Introduction
Pricing decisions significantly impact retail demand. TimeGPT makes it possible to forecast product demand while incorporating price as a key factor, enabling retailers to evaluate how different pricing scenarios might affect sales. This approach offers valuable insights for strategic pricing decisions. This tutorial demonstrates how to use TimeGPT for scenario analysis by forecasting demand under various pricing conditions. You’ll learn to incorporate price data into forecasts and compare different pricing strategies to understand their impact on consumer demand.What You’ll Learn
- How to forecast retail demand using price as an exogenous variable
- How to run what-if scenarios with different pricing strategies
- How to compare baseline, increased, and decreased price forecasts
- How to interpret price sensitivity in demand forecasts
How to Forecast Sales with Pricing Scenarios
Step 1: Import required packages
Import the packages needed for this tutorial and initialize your Nixtla client:Step 2: Load the M5 dataset
Let’s see an example on predicting sales of products of the M5 dataset. The M5 dataset contains daily product demand (sales) for 10 retail stores in the US. First, we load the data usingdatasetsforecast. This returns:
Y_df, containing the sales (ycolumn), for each unique product (unique_idcolumn) at every timestamp (dscolumn).X_df, containing additional relevant information for each unique product (unique_idcolumn) at every timestamp (dscolumn).
| unique_id | ds | y |
|---|---|---|
| FOODS_1_001_CA_1 | 2011-01-29 | 3.0 |
| FOODS_1_001_CA_1 | 2011-01-30 | 0.0 |
| FOODS_1_001_CA_1 | 2011-01-31 | 0.0 |
| FOODS_1_001_CA_1 | 2011-02-01 | 1.0 |
| FOODS_1_001_CA_1 | 2011-02-02 | 4.0 |
| FOODS_1_001_CA_1 | 2011-02-03 | 2.0 |
| FOODS_1_001_CA_1 | 2011-02-04 | 0.0 |
| FOODS_1_001_CA_1 | 2011-02-05 | 2.0 |
| FOODS_1_001_CA_1 | 2011-02-06 | 0.0 |
| FOODS_1_001_CA_1 | 2011-02-07 | 0.0 |
sell_price. This column shows the selling price of the product, and we expect demand to fluctuate given a different selling price.
| unique_id | ds | sell_price |
|---|---|---|
| FOODS_1_001_CA_1 | 2011-01-29 | 2.0 |
| FOODS_1_001_CA_1 | 2011-01-30 | 2.0 |
| FOODS_1_001_CA_1 | 2011-01-31 | 2.0 |
| FOODS_1_001_CA_1 | 2011-02-01 | 2.0 |
| FOODS_1_001_CA_1 | 2011-02-02 | 2.0 |
| FOODS_1_001_CA_1 | 2011-02-03 | 2.0 |
| FOODS_1_001_CA_1 | 2011-02-04 | 2.0 |
| FOODS_1_001_CA_1 | 2011-02-05 | 2.0 |
| FOODS_1_001_CA_1 | 2011-02-06 | 2.0 |
| FOODS_1_001_CA_1 | 2011-02-07 | 2.0 |
Step 3: Forecast demand using price as an exogenous variable
In this example, we forecast for a single product (FOODS_1_129_) across all 10 stores. This product exhibits frequent price changes, making it ideal for modeling price effects on demand. Learn more about using exogenous variables in TimeGPT.
y) and price (sell_price) data into one DataFrame:
| unique_id | ds | y | sell_price |
|---|---|---|---|
| FOODS_1_129_CA_1 | 2011-02-01 | 1.0 | 6.22 |
| FOODS_1_129_CA_1 | 2011-02-02 | 0.0 | 6.22 |
| FOODS_1_129_CA_1 | 2011-02-03 | 0.0 | 6.22 |
| FOODS_1_129_CA_1 | 2011-02-04 | 0.0 | 6.22 |
| FOODS_1_129_CA_1 | 2011-02-05 | 1.0 | 6.22 |
| FOODS_1_129_CA_1 | 2011-02-06 | 0.0 | 6.22 |
| FOODS_1_129_CA_1 | 2011-02-07 | 0.0 | 6.22 |
| FOODS_1_129_CA_1 | 2011-02-08 | 0.0 | 6.22 |
| FOODS_1_129_CA_1 | 2011-02-09 | 0.0 | 6.22 |
| FOODS_1_129_CA_1 | 2011-02-10 | 3.0 | 6.22 |
y, of these products has evolved in the last year of data.
Historical retail demand showing intermittent sales patterns across 10 stores
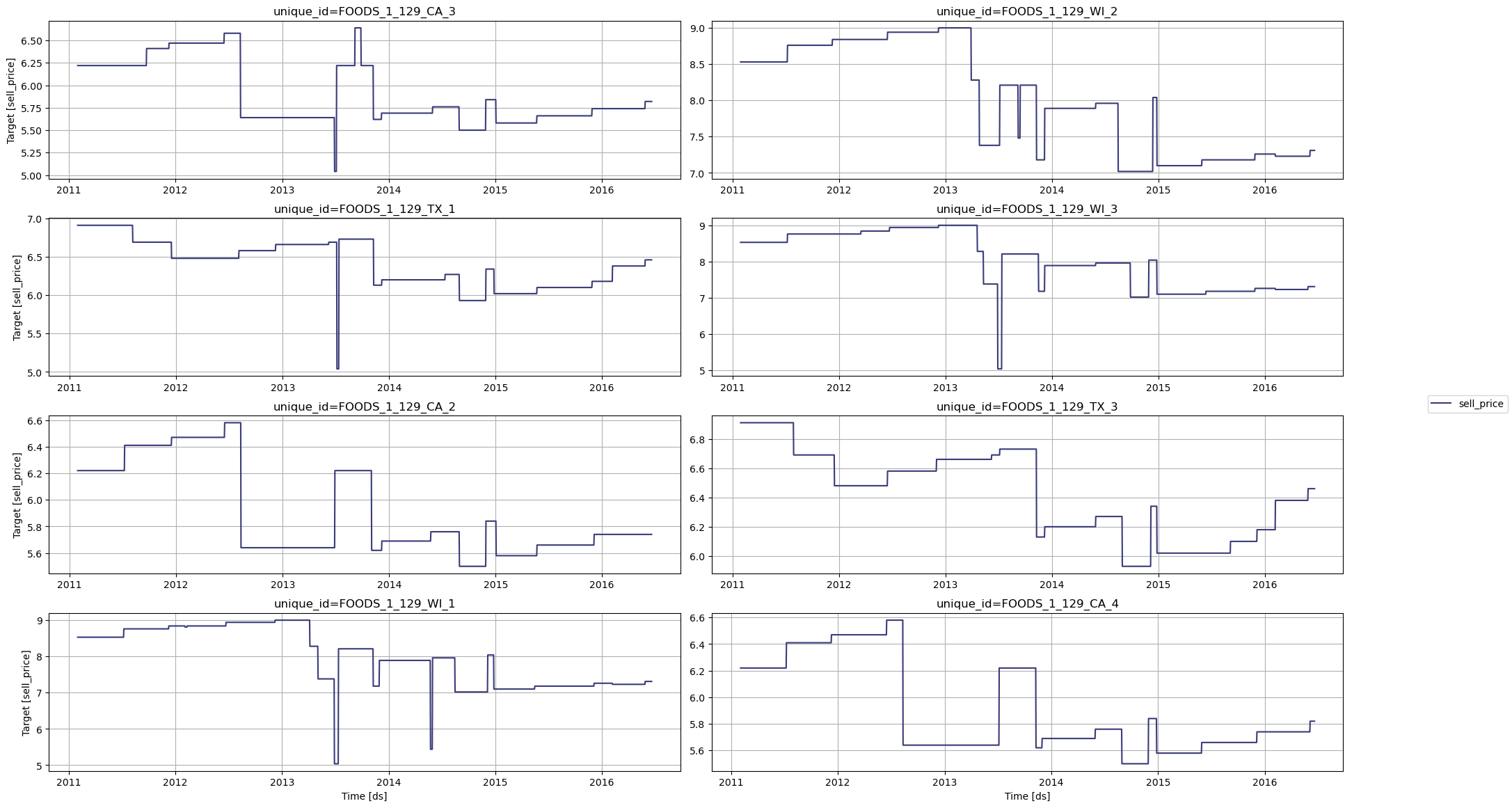
sell_price of these products across the entire data available.

Historical pricing trends showing price changes over 5 years for retail products
sell_price exogenous variable in TimeGPT, we have to add it as future values. Therefore, we create a future values dataframe, that contains the unique_id, the timestamp ds, and sell_price.
| unique_id | ds | sell_price |
|---|---|---|
| FOODS_1_129_CA_1 | 2016-05-23 | 5.74 |
| FOODS_1_129_CA_1 | 2016-05-24 | 5.74 |
| FOODS_1_129_CA_1 | 2016-05-25 | 5.74 |
| FOODS_1_129_CA_1 | 2016-05-26 | 5.74 |
| FOODS_1_129_CA_1 | 2016-05-27 | 5.74 |
| FOODS_1_129_CA_1 | 2016-05-28 | 5.74 |
| FOODS_1_129_CA_1 | 2016-05-29 | 5.74 |
| FOODS_1_129_CA_1 | 2016-05-30 | 5.74 |
| FOODS_1_129_CA_1 | 2016-05-31 | 5.74 |
| FOODS_1_129_CA_1 | 2016-06-01 | 5.74 |
| unique_id | ds | y | sell_price |
|---|---|---|---|
| FOODS_1_129_WI_3 | 2016-05-13 | 3.0 | 7.23 |
| FOODS_1_129_WI_3 | 2016-05-14 | 1.0 | 7.23 |
| FOODS_1_129_WI_3 | 2016-05-15 | 2.0 | 7.23 |
| FOODS_1_129_WI_3 | 2016-05-16 | 3.0 | 7.23 |
| FOODS_1_129_WI_3 | 2016-05-17 | 1.0 | 7.23 |
| FOODS_1_129_WI_3 | 2016-05-18 | 2.0 | 7.23 |
| FOODS_1_129_WI_3 | 2016-05-19 | 3.0 | 7.23 |
| FOODS_1_129_WI_3 | 2016-05-20 | 1.0 | 7.23 |
| FOODS_1_129_WI_3 | 2016-05-21 | 0.0 | 7.23 |
| FOODS_1_129_WI_3 | 2016-05-22 | 0.0 | 7.23 |
| unique_id | ds | TimeGPT |
|---|---|---|
| FOODS_1_129_CA_1 | 2016-05-23 | 0.875594 |
| FOODS_1_129_CA_1 | 2016-05-24 | 0.777731 |
| FOODS_1_129_CA_1 | 2016-05-25 | 0.786871 |
| FOODS_1_129_CA_1 | 2016-05-26 | 0.828223 |
| FOODS_1_129_CA_1 | 2016-05-27 | 0.791228 |

TimeGPT baseline forecast with 28-day ahead predictions for retail demand
Step 4: What-If Scenario Forecasting with Price Changes
What happens when we change the price of the products in our forecast period? Let’s see how our forecast changes when we increase and decrease thesell_price by 5%.
| unique_id | ds | TimeGPT | TimeGPT-sell_price_plus_5% | TimeGPT-sell_price_minus_5% |
|---|---|---|---|---|
| FOODS_1_129_CA_1 | 2016-05-23 | 0.875594 | 0.847006 | 1.370029 |
| FOODS_1_129_CA_1 | 2016-05-24 | 0.777731 | 0.749142 | 1.272166 |
| FOODS_1_129_CA_1 | 2016-05-25 | 0.786871 | 0.758283 | 1.281306 |
| FOODS_1_129_CA_1 | 2016-05-26 | 0.828223 | 0.799635 | 1.322658 |
| FOODS_1_129_CA_1 | 2016-05-27 | 0.791228 | 0.762640 | 1.285663 |
| FOODS_1_129_CA_1 | 2016-05-28 | 0.819133 | 0.790545 | 1.313568 |
| FOODS_1_129_CA_1 | 2016-05-29 | 0.839992 | 0.811404 | 1.334427 |
| FOODS_1_129_CA_1 | 2016-05-30 | 0.843070 | 0.814481 | 1.337505 |
| FOODS_1_129_CA_1 | 2016-05-31 | 0.833089 | 0.804500 | 1.327524 |
| FOODS_1_129_CA_1 | 2016-06-01 | 0.855032 | 0.826443 | 1.349467 |

What-if scenario comparison showing demand forecasts under different pricing strategies
Conclusion
What-if forecasting with TimeGPT enables data-driven pricing decisions by:- Modeling demand sensitivity to price changes
- Comparing multiple pricing scenarios simultaneously
- Incorporating exogenous variables for realistic predictions
Next Steps
- Explore intermittent demand forecasting with TimeGPT
- Learn about fine-tuning models for better accuracy
- Understand cross-validation for model evaluation
- Scale forecasts with distributed computing
Important Considerations
- This method assumes that historical demand and price behaviour is predictive of future demand, and omits other factors affecting demand. To include these other factors, use additional exogenous variables that provide the model with more context about the factors influencing demand.
- This method is sensitive to unmodelled events that affect the demand, such as sudden market shifts. To include those, use additional exogenous variables indicating such sudden shifts if they have been observed in the past too.